Amy Sprague
March 23, 2020
This is an important design tool to give engineers a target to shoot for, especially as we seek to fly more difficult missions to the Moon, Mars, the moons of Jupiter and beyond. – Danylo Malyuta
 Danylo Malyuta, lead author of the award-winning paper that applied convex optimization to the transposition and docking maneuver of the Apollo 11 mission.
Danylo Malyuta, lead author of the award-winning paper that applied convex optimization to the transposition and docking maneuver of the Apollo 11 mission.
What we gain by applying optimization algorithms to the iconic mission.
The 1969 Apollo 11 mission to the Moon is providing lasting impacts beyond the inspiration and wonder it inspired. It is still, fifty years later, providing valuable research data. Researchers from A&A’s Autonomous Control Lab and RAIN Lab accessed its trajectories and fuel usage data to validate the use of convex optimization algorithms in planning future spaceflights.
Specifically, they analyzed a thirty minute segment of the flight called the “transposition and docking” maneuver, which was the separation of the Command and Service Module from the Saturn V rocket. This maneuver extracted the lunar module in preparation for the moon landing by astronauts Neil Armstrong and Buzz Aldrin. During the historic mission, this maneuver burned through 50 kilograms of fuel.
NASA engineers in 1969 did not have the computing capability to apply convex optimization to make maneuvers more efficient. Today, however, A&A researchers, led by Ph.D. student Danylo Malyuta, took the opportunity to validate the use of such algorithms in spaceflight planning by applying them to this critical segment of the Apollo 11 mission.
In a paper that won the AIAA SciTech 2020 award for best graduate paper in Guidance, Navigation, and Controls, results showed that applying convex optimization algorithms to the targeted maneuver would save over 90 percent of fuel, bringing the fuel spent down to only seven kilograms.
We recently spoke with Danylo about the research, the results and the implications of this research.
First of all, what is convex optimization?
Convex optimization is a special method for arriving at the best decision when operating with conflicting constraints. You’re essentially trying to minimize some function that describes what you want, subject to a number of constraints that you must satisfy. In convex optimization, the function that you are trying to minimize looks like a parabola. Basically, the function “smiles” at you on a graph.
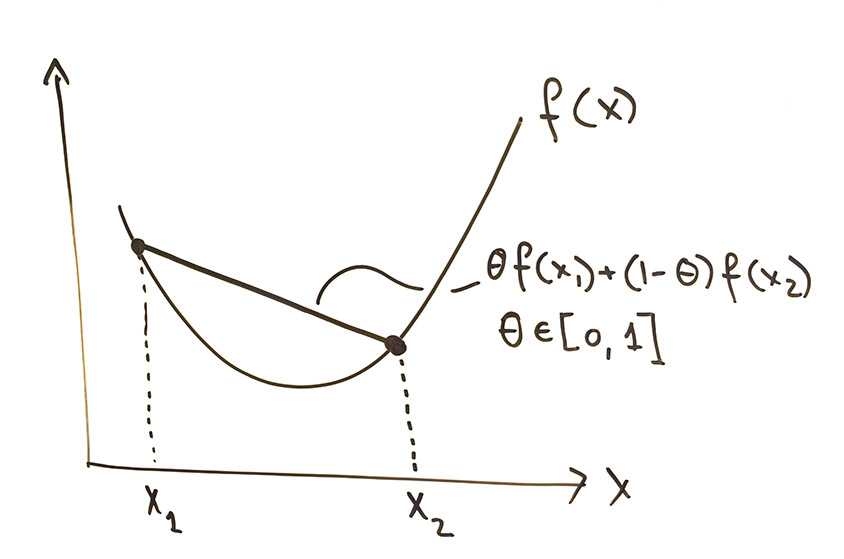
We start by entering constraints into a computer program and defining what is to be solved. Then, the program does the work for us, if it is convex, that is. But not every problem is convex. And it turns out that calculating the Apollo 11 trajectory is not convex, but we have a workaround. We use an iterative method called “successive convexification” which solves a number of convex optimization subproblems, maybe ten to twenty, in order to arrive at the solution.
How is it applied to space missions?
A common task in space mission design is to calculate the planned route, including any maneuvers, to the destination. This is known as trajectory design.
The proposed trajectory would have to satisfy certain constraints like the limits on how fast the craft can shift and rotate while keeping the cargo and systems safe and functioning. Another important constraint is the maximum and minimum allowed thrust from the engines. Then, a planned trajectory must minimize some variable, in this case fuel consumption.
During Apollo 11, digital computing was still in its infancy and was unable to handle computationally demanding tasks like optimization. Today, however, we can optimize difficult tasks very quickly. For our research on Apollo 11, we took into account constraints on spacecraft rotation, engine firing duration, and exhaust streams on the lunar module, all while seeking to minimize the fuel consumption.
Why is this research significant?
Right now, a lot of trajectory design at NASA and many of the space companies is done manually. By using convex optimization to create targets for this human design, we will be able to get closer to the ideal for safety, speed, efficiency, cost, and other constraints.
Computing an “optimal” trajectory helps engineers have a target to aim for even if manual operations will be in effect. So if the manually plotted trajectory is way off from what the algorithms are suggesting, we know we need to go back to the drawing board.
This is an important design tool to give engineers a target to shoot for, especially as we seek to fly more difficult missions to the Moon, Mars, the moons of Jupiter and beyond. Many of these missions will not be crewed, so our use of algorithms needs to be even more robust to adjust to many unforeseen conditions.
Our algorithms in this research told us that the part of the Apollo 11 mission that we analyzed could have been 90 percent more fuel efficient. If NASA engineers in 1969 knew this, they could have reworked their mission plan. Thanks to decades of computer and optimization advancement since Apollo, it is something we can do today.
For more information, see Fast Trajectory Optimization via Successive Convexification for Spacecraft Rendezvous with Integer Constraints by Danylo Malyuta, Taylor Reynolds, Michael Szmuk, Behçet Açikmeşe and Mehran Mesbahi